



Next: Sample Distributions
Up: Statistical Definitions
Previous: Regression Diagnostics
Contents
Subsections
PCA is essentialy an operation that rotates and scales the
axes of the variable space to maximize the variance. Since
rotation and scaling are linear the PCA operation
maintains linear relationships in the data. PCA is basically an
ordination
technique that consists of doing an eigenanalysis of the
correlation or covariance matrix. The underlying aim of PCA is to reduce
the dimensionality of the orignal dataset but retain most of the
original variability. A really neat example can be found
here
The resultant principal components are effectively new axes for the
data. Thus they are orthogonal and uncorrelated.
PCA is often motivated by the search for latent variables. Often it is
relatively easy to label the highest or second highest components,
but it becomes increasingly difficult as less relevant axes are
examined. The objects with the highest loadings (see below) or projections on
the axes (i.e. those which are placed towards the extremities of the
axes) are usually worth examining: the axis may be characterisable as
a spectrum running from a small number of objects with high positive
loadings to those with high negative loadings.
Also see Principal Components
Regression
The procedeure to carry out a PCA on a given set of data involves find
the eigenvectors and eigenvalues of the covariance or correlation
matrix. The data should be normalized (autoscaled) so as to remove
the effects of large differences in order. The resultant eigenvectors
are known as loadings and are coefficients for calculating linear
combinations of original variables (scores). The eigenvalues give
the variances of principal component scores. The algorithm can be
summarized as
Once we have the eigenvectors and eigenvalues we can transform the
original dataset by projecting the original points onto the new axes.
In the case of molecular descriptors the algorithm is
- Consider a molecule 1 which is described by a vector of
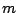 descriptors
descriptors
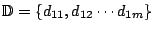 . Also the loading
matrix,
. Also the loading
matrix,
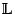 obtained will be a
obtained will be a
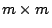 matrix with the
eigenvectors in the columns (so
matrix with the
eigenvectors in the columns (so
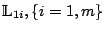 is the
eigenvector for the first PC)
is the
eigenvector for the first PC)
- Thus the projection of the original descriptor vector along
the first PC will be given by
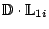
- Repeat for all the molecules and all the PC's
Once we have obtained the principal components (also termed as factors)
we need to decide on how many to consider. In general this is
empirically chosen as the number of components that comprise 95% of the
total variance. However there are two other methods
- The Kaiser criterion which says that one should only
retain factors whose corresponding eigenvalues are greater than 1.
This method can sometimes lead to too many factors being taken
- The scree method in which we plot the serial number
of an eigenvalue versus its actual value. Looking at this plot one
finds the point to the right of which the plot more or less flattens
out. All points to the left (this point inclusive) are chosen. This
method can sometimes lead to too few factors being chosen
The defining
characteristic then that distinguishes between the two factor analytic
models is that in principal components analysis we assume that all
variability in an item should be used in the analysis, while in
principal factors analysis we only use the variability in an item
that it has in common with the other items. In most
cases, these two methods usually yield very similar results. However,
principal components analysis is often preferred as a method for data
reduction, while principal factors analysis is often preferred when
the goal of the analysis is to detect structure
If, in the correlation matrix there are variables that are 100%
redundant, then the inverse of the matrix cannot be computed. For
example, if a variable is the sum of two other variables selected for
the analysis, then the correlation matrix of those variables cannot
be inverted, and the factor analysis can basically not be performed.
The problem can be overcome by artificially lowering all correlations
in the correlation matrix by adding a small constant to the diagonal of
the matrix, and then restandardizing it. This procedure will usually
yield a matrix that now can be inverted and thus factor-analyzed;
moreover, the factor patterns should not be affected by this
procedure. However, note that the resulting estimates are not exact.




Next: Sample Distributions
Up: Statistical Definitions
Previous: Regression Diagnostics
Contents
2003-08-29