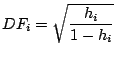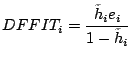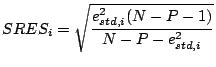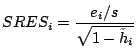Next: Principal Components Analysis
Up: Statistical Definitions
Previous: Regression Statistics
Contents
Subsections
The definitions here are from taken from the ADAPT manual and when
not in the manual from the ADAPT source. They
possibly differ from textbook definitions. I go with what ADAPT
gives me!
Leverage
These are the diagonal elements for the hat matrix which is defined as
A given diagonal element 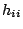 represents the distance between
represents the distance between
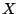 values for the i'th observation and the means of all
values for the i'th observation and the means of all 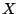 values. A
large leverage value indicates that the ith observation is distant
from the center of the
values. A
large leverage value indicates that the ith observation is distant
from the center of the 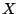 observations. Alternatively it is used
in determining the impact of a y value in predicting itself. A
leverage is considered high is it is greater than 4p/n (p is number
of descriptors + 1 and n is number of observations). See
Belsley, Kuh and Welsch, Regression
Diagnostics.
where
observations. Alternatively it is used
in determining the impact of a y value in predicting itself. A
leverage is considered high is it is greater than 4p/n (p is number
of descriptors + 1 and n is number of observations). See
Belsley, Kuh and Welsch, Regression
Diagnostics.
where 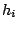 is the
leverage
for the i'th case and
is the
leverage
for the i'th case and 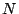 is the number of observations
is the number of observations
One can think of the independent variables (in a regression
equation) as defining a multidimensional space in which
each observation can be plotted. Also, one can plot a point
representing the means for all independent variables. This
"mean point" in the multidimensional space is also called
the centroid. The Mahalanobis distance is the distance of a
case from the centroid in the multidimensional space, defined
by the correlated independent variables (if the independent
variables are uncorrelated, it is the same as the simple Euclidean
distance). Thus, this measure provides an indication of whether or
not an observation is an outlier with respect to the independent
variable values. See Belsley, Kuh and Welsch, Regression
Diagnostics.
Cook's Distance
This definition is taken from ADAPT:
where 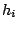 is the
leverage
for the i'th case,
is the
leverage
for the i'th case,
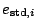 is
the
standardized residual
and
is
the
standardized residual
and 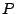 is the number of descriptors.
is the number of descriptors.
This is another measure of impact of the respective case on
the regression equation. It indicates the difference between
the computed
B values
(ie the regression coefficients) and the
values one would have obtained, had the respective case been
excluded. All distances should be of about equal magnitude; if
not, then there is reason to believe that the respective case(s)
biased the estimation of the
regression coefficients. See Neter, Wasserman, Kutner, Applied Linear
Statistical Models, 2nd Edition, pg 408; Technometrics, 19,
1977, pg 15.
DFITS provides a measure of the difference in the estimated i'th y
value when the regression is recalculated without using the i'th y
value.
where 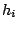 is the
leverage
for the i'th case. An important
point to note is that ADAPT outputs the values calculated using
the above formula labeled by DFFIT. However
StatSoft
Inc.
defines
DFFIT using the following formula:
where
is the
leverage
for the i'th case. An important
point to note is that ADAPT outputs the values calculated using
the above formula labeled by DFFIT. However
StatSoft
Inc.
defines
DFFIT using the following formula:
where 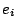 is the
residual for the i'th case (i.e. the
residual) and
is the
residual for the i'th case (i.e. the
residual) and
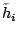 is defined as
is defined as
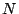 being the total number of cases. A DFITS value is considered
large if its absolute value is larger than
being the total number of cases. A DFITS value is considered
large if its absolute value is larger than
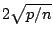 where p is
the number of parameters (descriptors) + 1 and n is the number of
observations (ie number of molecules).
where p is
the number of parameters (descriptors) + 1 and n is the number of
observations (ie number of molecules).
Residual
Fancy term for the error in the predicted value compared to the
observed value. Defined as:
where 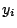 is the i'th observed value and
is the i'th observed value and
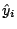 is the i'th predicted value.
is the i'th predicted value.
Standardized Residual
Defined as:
where 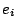 is the residual
is the residual
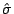 is the XXX and
is the XXX and 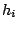 is the
leverage
for the i'th case. As usual the ADAPT definition
does'nt match the textbook one.
StatSoft
Inc.
defines it by:
where
is the
leverage
for the i'th case. As usual the ADAPT definition
does'nt match the textbook one.
StatSoft
Inc.
defines it by:
where 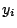 is the i'th observed value and
is the i'th observed value and
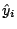 is the i'th predicted value.
is the i'th predicted value.
Studentized Residual
where 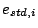 is the
standardized residual
for the i'th
case, N is the number of observations and P is the number of
descriptors. Once again
StatSoft
Inc.
defines
is the
standardized residual
for the i'th
case, N is the number of observations and P is the number of
descriptors. Once again
StatSoft
Inc.
defines 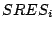 in a
slightly different manner:
where
in a
slightly different manner:
where 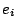 is the
residual
and
is the
residual
and
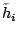 is defined as
is defined as
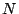 being the total number of cases. I cant seem to find what
being the total number of cases. I cant seem to find what 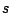 stands for
stands for




Next: Principal Components Analysis
Up: Statistical Definitions
Previous: Regression Statistics
Contents
2003-08-29
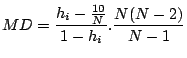
![$\displaystyle D_{i}^{\mathrm{cook}} = \frac{e_{\mathrm{std},i}^{2}}{P}
\left[ \frac{h_{i}}{1 - h_{i}} \right]
$](img72.png)