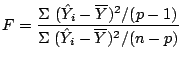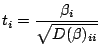Next: Regression Diagnostics
Up: Statistical Definitions
Previous: Correlation Coefficient
Contents
Subsections
B & Beta Coefficients
In regression, B coefficients
are the raw regression coefficients. They represent the independent
contributions of each independent variable to the prediction of
the dependent variable. However, their values may not be comparable
between variables because they depend on the units of measurement
or ranges of the respective variables. Beta coefficients arcients
are the regression coefficients you would have obtained had you
first standardized all of your variables to a mean of 0 and a
standard deviation of 1. Thus, the advantage of Beta coefficients
(as compared to B coefficients which are not standardized)
is that the magnitude of these Beta coefficients allow you to
compare the relative contribution of each independent variable
in the prediction of the dependent variable.
This is also denoted by  - and in general is termed as
the weighted sums of squared residuals. In the case of ADAPT the
fitting is non weighted and so it condenses to sum of squared
residuals. Defined as:
where
- and in general is termed as
the weighted sums of squared residuals. In the case of ADAPT the
fitting is non weighted and so it condenses to sum of squared
residuals. Defined as:
where
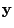 is the observations vector (ie dependant
variable values),
is the observations vector (ie dependant
variable values),
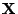 is the
is the 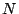 by
by 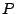 matrix
of predictor variables (ie values for P descriptors for N
molecules),
matrix
of predictor variables (ie values for P descriptors for N
molecules),
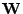 is the weight matrix, which for ADAPT
is the identity matrix and
is the weight matrix, which for ADAPT
is the identity matrix and
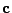 is the vector of
is the vector of 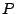 unknown best fit parameters (ie the regression coefficients
which we are trying to find).
Basically the best fit is found by minimizing the value of
unknown best fit parameters (ie the regression coefficients
which we are trying to find).
Basically the best fit is found by minimizing the value of 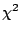 .
The overall
F statistic
tests the null hypothesis
where p is the number of parameters. Note that that above equation
does not include the intercept coefficient (
.
The overall
F statistic
tests the null hypothesis
where p is the number of parameters. Note that that above equation
does not include the intercept coefficient (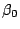 ).
It is defined by the equation
where
If
).
It is defined by the equation
where
If 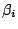 is the i'th parameter then
t statistic
tests the null hypothesis
is the i'th parameter then
t statistic
tests the null hypothesis
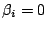 . It is calculated by,
where
. It is calculated by,
where 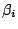 is defined above and
is defined above and
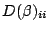 is the
diagonal element of the covariance matrix corresponding to the i'th
parameter. The statistic is assumed to follow the
T distribution
with (n-p) degrees of freedom (n is the number of observations and
p is the number of parameters).
(Source).
is the
diagonal element of the covariance matrix corresponding to the i'th
parameter. The statistic is assumed to follow the
T distribution
with (n-p) degrees of freedom (n is the number of observations and
p is the number of parameters).
(Source).




Next: Regression Diagnostics
Up: Statistical Definitions
Previous: Correlation Coefficient
Contents
2003-08-29