A 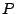 is the lowest level (of significance) at which the
observed value of the test is significant.
It is equal to the significance level of the test for which
we would only just reject the null hypothesis. The
is the lowest level (of significance) at which the
observed value of the test is significant.
It is equal to the significance level of the test for which
we would only just reject the null hypothesis. The 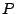 value is
compared with the actual significance level of our test and,
if it is smaller, the result is significant. That is, if the
null hypothesis were to be rejected at the 5% signficance
level, this would be reported as
value is
compared with the actual significance level of our test and,
if it is smaller, the result is significant. That is, if the
null hypothesis were to be rejected at the 5% signficance
level, this would be reported as
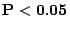
Small 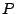 values suggest that the null hypothesis is unlikely to be
true. The smaller it is, the more convincing is the rejection of
the null hypothesis. It indicates the strength of evidence for say,
rejecting the null hypothesis
values suggest that the null hypothesis is unlikely to be
true. The smaller it is, the more convincing is the rejection of
the null hypothesis. It indicates the strength of evidence for say,
rejecting the null hypothesis 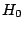 , rather than simply concluding
Reject
, rather than simply concluding
Reject 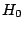 or Do not reject
or Do not reject 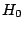
![]() values suggest that the null hypothesis is unlikely to be
true. The smaller it is, the more convincing is the rejection of
the null hypothesis. It indicates the strength of evidence for say,
rejecting the null hypothesis
values suggest that the null hypothesis is unlikely to be
true. The smaller it is, the more convincing is the rejection of
the null hypothesis. It indicates the strength of evidence for say,
rejecting the null hypothesis ![]() , rather than simply concluding
Reject
, rather than simply concluding
Reject ![]() or Do not reject
or Do not reject ![]()