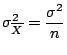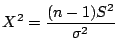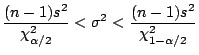Next: Testing Hypotheses
Up: Statistical Definitions
Previous: Sample Distributions
Contents
Subsections
Some definitions
Even efficient estimators will have some error when they estimate
the value of a population parameter. In many cases it is better to know
an interval within which the population parameter can be found. This
type of estimate is termed as an interval estimate, ie we say
that the population parameters lies within the interval
Some features of interval estimates
Since
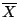 has a sampling distribution centered at
has a sampling distribution centered at 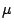 (the
population mean) it has a variance smaller than other
estimators of
(the
population mean) it has a variance smaller than other
estimators of 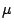 . Furthermore since the variance of
. Furthermore since the variance of
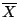 is
defined as
is
defined as
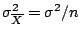 , the variance
decreases with larger sample sizes. Thus
, the variance
decreases with larger sample sizes. Thus
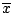 is the best point
estimate of
is the best point
estimate of 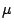
Considering interval estimates we know that the Central Limit
Theorem says that the sampling
distribution of
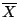 is approximately normal with mean
is approximately normal with mean
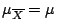 and standard deviation
and standard deviation
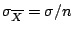 . Thus if
. Thus if
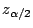 is the z value above
which we get an area of
is the z value above
which we get an area of
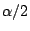 then we can write
then we can write
and since Z is defined as
we can substitute and manipulate to get
Essentaially this says that if
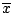 is the mean of a
random sample of size
is the mean of a
random sample of size 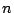 taken from a population with mean
taken from a population with mean
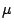 and standard deviation
and standard deviation 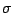 then the
then the
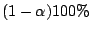 confidence interval for
confidence interval for 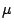 is given by
Thus the values of
is given by
Thus the values of
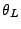 and
and
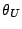 are the left
and right sides of the inequality.
are the left
and right sides of the inequality.
Thus for the mean we can say that if
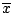 is an
estimator of
is an
estimator of 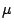 then we can be
then we can be
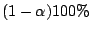 sure that
the error (ie
sure that
the error (ie
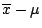 ) will not exceed
) will not exceed
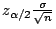
The number of members in a sample required to achieve a
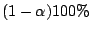 confidence level for an error
confidence level for an error 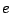 (ie
(ie
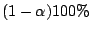 sure that the error will not exceed
sure that the error will not exceed
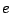 ) is given by
) is given by
When we have a sample from a normal distribution with an unknown
standard deviation then the variable defined as
has a t distribution with
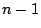 degrees of freedom. Proceeding as above we can conclude that if
degrees of freedom. Proceeding as above we can conclude that if
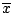 and
and 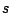 are the sample mean and standard deviation of a
sample from a normal population with unknown variance then a
are the sample mean and standard deviation of a
sample from a normal population with unknown variance then a
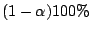 confidence interval for
confidence interval for 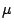 is given by
where
is given by
where
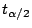 is a t value with
is a t value with 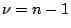 degrees of freedom.
degrees of freedom.
An important feature is when 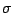 is known we can use the Central Limit
Theorem (ie a normal
distribution) and when
is known we can use the Central Limit
Theorem (ie a normal
distribution) and when 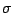 is
unknown we use the sampling distribution of T (ie a t
distribution). In many
cases when
is
unknown we use the sampling distribution of T (ie a t
distribution). In many
cases when 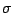 is unknown and
is unknown and 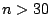
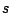 can be used instead of
can be used instead of 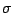 to give the interval
to give the interval
This is termed as the large sample confidence interval
We know that the variance of the estimator
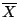 is
The standard deviation of
is
The standard deviation of
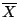 is also termed as the
standard error. Thus confidence intervals can also be written
as
is also termed as the
standard error. Thus confidence intervals can also be written
as
- Width of the confidence interval depends on the standard error of
the estimate
- Alternatively the width of the confidence interval depends on the
quality of the estimate
When using 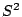 as an estimator for the population
as an estimator for the population
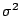 we
can get an interval estimate of
we
can get an interval estimate of
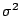 by the statistic
which has a
by the statistic
which has a 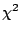 distribution with
distribution with 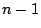 degrees of freedom (when
the samples are taken from a normal population). Rearranging and
proceeding as before we get
degrees of freedom (when
the samples are taken from a normal population). Rearranging and
proceeding as before we get




Next: Testing Hypotheses
Up: Statistical Definitions
Previous: Sample Distributions
Contents
2003-08-29
![]() is approximately normal with mean
is approximately normal with mean
![]() and standard deviation
and standard deviation
![]() . Thus if
. Thus if
![]() is the z value above
which we get an area of
is the z value above
which we get an area of
![]() then we can write
then we can write
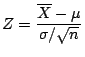
![]() is an
estimator of
is an
estimator of ![]() then we can be
then we can be
![]() sure that
the error (ie
sure that
the error (ie
![]() ) will not exceed
) will not exceed
![]()
![]() confidence level for an error
confidence level for an error ![]() (ie
(ie
![]() sure that the error will not exceed
sure that the error will not exceed
![]() ) is given by
) is given by
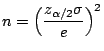
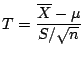
![]() is known we can use the Central Limit
Theorem (ie a normal
distribution) and when
is known we can use the Central Limit
Theorem (ie a normal
distribution) and when ![]() is
unknown we use the sampling distribution of T (ie a t
distribution). In many
cases when
is
unknown we use the sampling distribution of T (ie a t
distribution). In many
cases when ![]() is unknown and
is unknown and ![]()
![]() can be used instead of
can be used instead of ![]() to give the interval
to give the interval