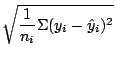Fundamental Definitions

Degrees of Freedom: The degrees of freedom of a set of observations are the number of values which could be assigned arbitrarily within the specification of the system. For example, in a sample of size n grouped into k intervals, there are k-1 degrees of freedom, because k-1 frequencies are specified while the other one is specified by the total size n. In some circumstances the term degrees of freedom is used to denote the number of independent comparisons which can be made between the members of a sample.

Standard Deviations: There are two types of standard deviations. The standard deviation of the population , denoted by $\sigma$, is defined as

$$\sigma = \sqrt \frac{\Sigma(x_{i} - \mu)^2}{N}$$

where $\mu$ is the population mean and $N$ is the population size. The sample estimate of the population standard deviation (sample SD) is denoted by $s$ and defined as

$$s = \sqrt \frac{\Sigma (x_{i} - \overline{x})^{2}}{n-1}$$

where $\overline{x}$ is the sample mean and $n$ is the sample size.

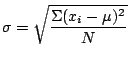
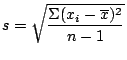
Variance: The square of the population standard deviation, ie $\sigma^{2}$. The square of the sample standard deviation ( $s^{2}$) is termed the sample estimate of the population variance.

Covariance Matrix Given $n$ sets of variates written as ${X_1} \cdots {X_n}$ (such as $n$ molecules each described by $m$ descriptors) then the first order covariance matrix is defined by

$$V_{ij} = cov(x_i,x_j)$$

$$= \langle (x_i - \mu_i) (x_j - \mu_j) \rangle$$

$$= \langle x_i x_j \rangle - \langle x_i \rangle \langle x_j \rangle$$

where $\mu_i = \langle x_i \rangle$, the mean of $x_i$. The statistical correlation is defined by

$$cor(x_i, x_j) = \frac{ cov(x_i, x_j) }{\sigma_i \sigma_j}$$

where $\sigma_i$ and $\sigma_j$ are the standard deviations. See Mathworld for more details.

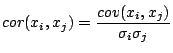
Root Mean Square Error: The individiual errors are squared, added, divided by the number of errors (ie, the number of observations) and the square rooted. It summarizes the overall error.

$$\sqrt{ \frac{1}{n_{i}} \Sigma (y_{i} - \hat{y}_{i})^{2}}$$

where $y_{i}$ is the predicted value, $\hat{y}_{i}$ is the observed value and $n_{i}$ is the number of observations.