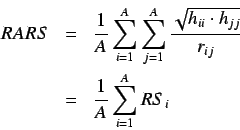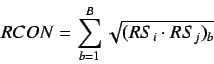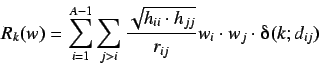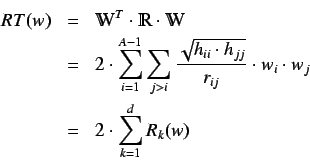Next: 3D MoRSE[15,10]
Up: Molecular Descriptors
Previous: Galvez Topological Charge Indices[7,8,9]
Contents
Subsections
The GETAWAY (GEometry, Topology, and Atom Weights AssemblY) try to
match 3D molecular geometry provided by the molecular influence
matrix and atom relatedness by topology with chemical information by
using different atomic weighting schemes (unit weights, mass,
polarizability, electronegativity).
The molecular influence matrix, 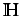 is defined by
is defined by
where 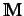 is the molecular matrix. The resultant
is the molecular matrix. The resultant 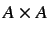 matrix is invariant to rotation of the molecular
coordinates. The diagonal elements
matrix is invariant to rotation of the molecular
coordinates. The diagonal elements 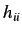 are termed leverages and
represent the influence of each atom in determining the shape of the
molecule. Each off diagonal element
are termed leverages and
represent the influence of each atom in determining the shape of the
molecule. Each off diagonal element 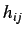 represents the degree of
of accessibility of the j'th atom to interactions with the i'th atom.
represents the degree of
of accessibility of the j'th atom to interactions with the i'th atom.
H-GETAWAY descriptors are obtained by manipulating the 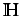 matrix
The simple H-GETAWAY is defined by
matrix
The simple H-GETAWAY is defined by
and is essentially the geometric mean of the leverage magnitude.
There are 3 types of informational
indices which consider the diagonal elements of 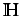 as indicative of molecular complexity (since they are sensitive
to the whole molecule structure).
as indicative of molecular complexity (since they are sensitive
to the whole molecule structure).
- Total information content
- Standardized information content on the
leverage equality
represented by,
where 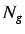 is the number of atoms with the same leverage value
and
is the number of atoms with the same leverage value
and 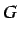 is the number of equivilance classes into which the atoms
are partitioned according to leverage equality and
is the number of equivilance classes into which the atoms
are partitioned according to leverage equality and 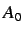 is the
number of non hydrogen atoms. These indices encode information
regarding the molecule entropy.
is the
number of non hydrogen atoms. These indices encode information
regarding the molecule entropy.
- Mean information content on the leverage
magnitude
is defined as
where 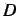 is the matrix rank defined by
is the matrix rank defined by
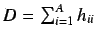 and
and 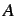 is the total number of atoms, hydrogens
included.
is the total number of atoms, hydrogens
included.
The H-GETAWAY autocorrelation descriptor utilizes the geometric
information implicit in the leverage values and atomic weighting
schemes to give rise to a new set of descriptors. By analogy
with the
Moreau - Broto descriptors the HATS indices are
defined by weighting each atom in a molecule by
thus giving a weight vector
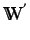 . The HATS are
then defined as
. The HATS are
then defined as
and
where 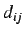 is the topological distance between the i'th and j'th
atoms and
is the topological distance between the i'th and j'th
atoms and
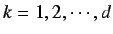 with
with
The HATS total index is defined by summing the individual
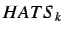 indices for increasing
indices for increasing 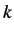 and is given by
and is given by
where 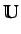 is the
is the 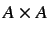 unit matrix.
This subset replaces
unit matrix.
This subset replaces 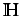 with other types of
matrices such as a combination of the molecular influence matrix
and the geometry matrix to give the influence/distance matrix,
with other types of
matrices such as a combination of the molecular influence matrix
and the geometry matrix to give the influence/distance matrix,
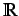 defined as
defined as
where 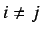 Using the elements of
Using the elements of  we can get several
descriptors
The average row sum of
we can get several
descriptors
The average row sum of 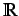 is defined as
is defined as
where 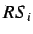 is the i'th row sum.
The
is the i'th row sum.
The 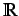 connectivity index is defined by analogy
with the Randic connectivity index and is defined as
connectivity index is defined by analogy
with the Randic connectivity index and is defined as
This descriptor is designed by analogy with the Lovasz-Pelikan
index and describes molecular branching and is defined as the
first eigenvalue of 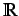 These are defined analogously to the H-GETAWAY autocorrelational
indices and so we have the w weighted k'th order
autocorrelation index
These are defined analogously to the H-GETAWAY autocorrelational
indices and so we have the w weighted k'th order
autocorrelation index
where
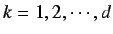 . We can also calculate the a R total
index defined as
. We can also calculate the a R total
index defined as




Next: 3D MoRSE[15,10]
Up: Molecular Descriptors
Previous: Galvez Topological Charge Indices[7,8,9]
Contents
2003-06-16
![]() is defined by
is defined by
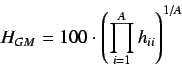
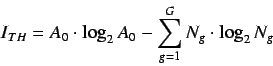
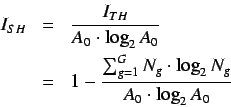
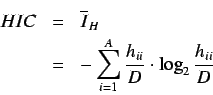
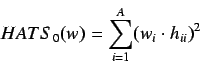
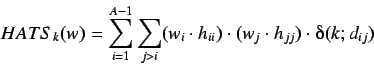
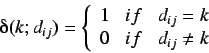
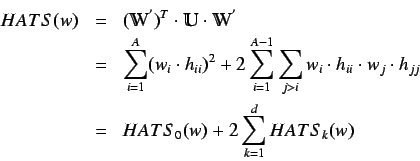
![\begin{displaymath}[ \varmathbb{R} ]_{ij} = \left[ \frac{\sqrt{h_{ii} \cdot
h_{jj}}}{r_{ij}} \right]_{ij}
\end{displaymath}](img85.png)