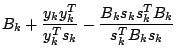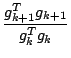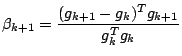: Maths
: Matrix Math
目次
Optimization
In general if 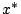 minimizes an unconstrained function
minimizes an unconstrained function 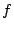 then
then 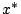 is a solution to the system of equations
is a solution to the system of equations
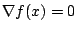 . The converse
is not always true. The solution to a set of equations
. The converse
is not always true. The solution to a set of equations
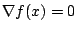 is termed the stationary point or critical point and may
be minimum, maximum or a saddle point. We can determine exactly which by
considering the Hessian matrix
is termed the stationary point or critical point and may
be minimum, maximum or a saddle point. We can determine exactly which by
considering the Hessian matrix 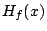 at
at 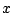 .
.
- If
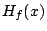 is positive definite then
is positive definite then 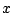 is a minimum of
is a minimum of 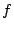
- If
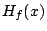 is negative definite then
is negative definite then 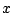 is a maximum of
is a maximum of 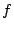
- If
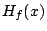 is indefinite then
is indefinite then 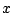 is a saddle point of
is a saddle point of 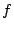
To check for definiteness we have the following options
- Compute the
Cholesky factorization. It will succeed only if
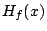 is positive definite
is positive definite
- Calculate the inertia of the matrix
- Calculate the eigenvalues and check whether they are all
positive or not
Golden Search
In this method the function is initially evaluate dat 3 points and a
quadratic polynomial is fitted to the resulting values. The minimum of
the parabola replaces the oldest of the initial point and the process
repeats.
Newton Methods
Another method for obtaining a local quadratic apporximation to a
function is to consider the truncated Taylor expansion of 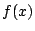 The minimum of this parabolic representation exists at
and so the iteration scheme is given by
Some important features include
The minimum of this parabolic representation exists at
and so the iteration scheme is given by
Some important features include
- Normally has quadratic convergence
- If started far from the desired solution it may fail to
converge or may converge to a maximum or a saddle point
Direct Search Method
In this method an 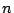 dimensional function
dimensional function
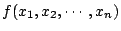 is
evaluated at
is
evaluated at 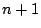 points. The move to a new point is made along the
line joining the worst current point and the centroid of the
points. The move to a new point is made along the
line joining the worst current point and the centroid of the 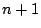 points. The new point replaces the worst point and we iterate
Some features include
points. The new point replaces the worst point and we iterate
Some features include
- Similar to a Golden Search since it involves comparison of
function values at different points
- Does not have the convergence gaurantee that a Golden Search
has
- Several parameters are involved such as how far to go along
the line and how to expand/contract the simplex depending on
whether the search was successful or not
- Good for when
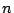 is small but ineffective when
is small but ineffective when 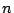 is larger
than 2 or 3
is larger
than 2 or 3
Steepest Descent Method
Using knowledge of the gradient can improve a search for minima. In this
method we realize that at a given point 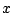 where the gradient is non
zero,
where the gradient is non
zero,
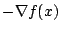 points in the direction of steepest descent for
the function
points in the direction of steepest descent for
the function 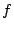 (ie, the function decreases more rapidly in this
direction than in any other direction). The iteration formula formula
starts with an initial guess
(ie, the function decreases more rapidly in this
direction than in any other direction). The iteration formula formula
starts with an initial guess 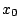 and then
where
and then
where 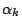 is a line search parameter and is obtained by
minimizing
with respect to
is a line search parameter and is obtained by
minimizing
with respect to 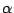
Newtons Method
This method involve use of both the first and second order derivatives
of a function. The iteration formula is
where 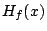 is the Hessian matrix. However rather than inverting
the matrix we obtain it by solving
for
is the Hessian matrix. However rather than inverting
the matrix we obtain it by solving
for 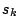 and then writing the iteration as
Some features include
and then writing the iteration as
Some features include
- Normally quadratic convergence
- Unreliable unless started close to the desired minima
There are two variations
- Damped Newton Method: When started far from the desired
solution the use of a line search parameter along the direction
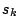 can make the method more robust. Once the iterations are
near the solution simply set
can make the method more robust. Once the iterations are
near the solution simply set
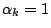 for subsequent
iterations
for subsequent
iterations
- Trust region methods: This involves maintaining an estimate of
the radius of a region in which the quadratic model is
sufficiently accurate
These methods are similar to Newtonian methods in that they use both
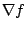 and
and 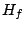 . However,
. However, 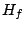 is usually approximated. The
general formula for iteration is given by
Some features of these types of methods include
is usually approximated. The
general formula for iteration is given by
Some features of these types of methods include
- Convergence is slightly slower than Newton methods
- Much less work per iteration
- More robust
- Some methods do not require evaluation of the second
derivatives at all
BFGS
The BFGS method is termed a secant updating method. The general
aim of these methods is to preserve symmetry of the approximate Hessian
as well as maintain positive definiteness. The former reduces workload
per iteration and the latter makes sure that a quasi Newton step is
always a descent direction.
We start with an initial guess 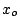 and a symmetric positive definite
approximate Hessian,
and a symmetric positive definite
approximate Hessian, 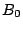 (which is usually taken as the identity
matrix). Then we iterate over the following steps
(which is usually taken as the identity
matrix). Then we iterate over the following steps
Some features include
- Usually a factorization of
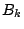 is updated rather than
is updated rather than
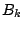 itself. This allows the linear system in Eq 1 to be solved
in
itself. This allows the linear system in Eq 1 to be solved
in
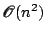 steps rather than
steps rather than
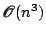
- No second derivatives are required
- Superlinear convergence
- A line search can be added to enhance the method
Conjugate Gradient
This method as above does not require the second derivative and in
addition does not even store an approximation to the Hessian. The
sequence of operations starts with an initial guess 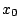 , and
initializes
, and
initializes
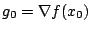 and
and
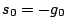 , then
, then
The update for 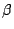 is given by Fletcher & Reeves. An alternative is
the Polak - Ribiere formula
Some features include
is given by Fletcher & Reeves. An alternative is
the Polak - Ribiere formula
Some features include
- This method uses gradients like the
steepest descent method
but avoids repeated searches by modifying the gradient at each
step to remove components in previous directions
- The algorithm is usually restarted after
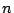 iterations
reinitializing to use the negative gradient at the current point
iterations
reinitializing to use the negative gradient at the current point




: Maths
: Matrix Math
目次
平成16年8月12日
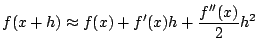
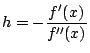
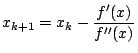
![]() and a symmetric positive definite
approximate Hessian,
and a symmetric positive definite
approximate Hessian, ![]() (which is usually taken as the identity
matrix). Then we iterate over the following steps
(which is usually taken as the identity
matrix). Then we iterate over the following steps