



: Optimization
: Maths
: 目次
目次
Singular Value Decomposition
The operation decomposes an
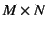 matrix (with
matrix (with 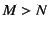 )
)
 into the
product of a
into the
product of a
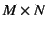 orthogonal matrix
orthogonal matrix
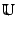 , an
, an
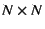 diagonal matrix of singular values,
diagonal matrix of singular values,
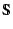 and the
transpose of an
and the
transpose of an
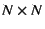 orthogonal square matrix
orthogonal square matrix
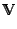 , thus
Some features of this decomposition include
, thus
Some features of this decomposition include
- The condition number of the matrix is given by the ratio of
the largest singular value to the smallest singular value.
- The presence of a zero singular value indicates that the matrix is singular
- The number of non-zero singular values indicates the rank of the matrix
Cholesky Factorization
Given a matrix
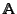 which is symmetric and positive definite we can do a
LU decomposition to give
However arranging such that
which is symmetric and positive definite we can do a
LU decomposition to give
However arranging such that
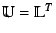 we get
we get
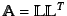 which is the
Cholesky factorization of
which is the
Cholesky factorization of 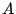 . The elements of
. The elements of 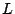 can be easily
determined by equating components. The utility of a Cholesky
factorization is that it convert the linear system
can be easily
determined by equating components. The utility of a Cholesky
factorization is that it convert the linear system
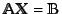 into two triangular systems which can be
solved by backward and forward substitutions. For the 2D case
This gives us
into two triangular systems which can be
solved by backward and forward substitutions. For the 2D case
This gives us
Given,
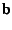 is a vector in
is a vector in
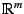 and
and 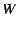 is a subspace of
is a subspace of
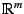 spanned by the vectors
spanned by the vectors
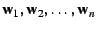 . We want to find the orthogonal projection of
. We want to find the orthogonal projection of
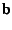 onto
onto 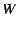 . Form the matrix
. Form the matrix
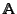 whose columns are the vectors
whose columns are the vectors
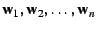 and then solve the
normal system
The solution vector
and then solve the
normal system
The solution vector
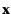 when premultiplied by
when premultiplied by
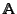 gives the orthogonal projection of
gives the orthogonal projection of
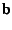 onto
onto 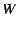 , i.e.,
, i.e.,
An alternative representation (from Mathworld) is that if the subspace
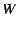 is represented by the orthonormal basis
is represented by the orthonormal basis
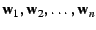 then the orthogonal projection
onto
then the orthogonal projection
onto 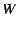 is given by
is given by
Here
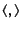 is termed the inner product and is the
generalization of the dot product.
is termed the inner product and is the
generalization of the dot product.
Yet another definition says that if
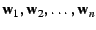 is the orthonormal basis for a
subspace
is the orthonormal basis for a
subspace 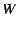 then
then
Note that this is valid when
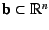 ,
i.e., the same space as
,
i.e., the same space as 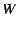 .
.




: Optimization
: Maths
: 目次
目次
平成16年8月12日
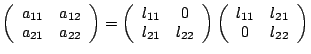
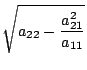
![]() is represented by the orthonormal basis
is represented by the orthonormal basis
![]() then the orthogonal projection
onto
then the orthogonal projection
onto ![]() is given by
is given by
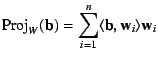
![]() is the orthonormal basis for a
subspace
is the orthonormal basis for a
subspace ![]() then
then