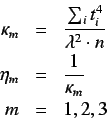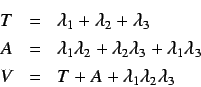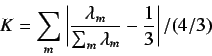Next: Bibliography
Up: Molecular Descriptors
Previous: 3D MoRSE[15,10]
Contents
Subsections
WHIM descriptors are based on statistical indices calculated on the
projections of atoms along principal axes (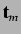 ). The aim is to capture
3D information regarding size, shape, symmetry and atom distributions
with respect to invariant reference frames.
). The aim is to capture
3D information regarding size, shape, symmetry and atom distributions
with respect to invariant reference frames.
The algorithm essentially carries out a PCA on the centered cartesian
coordinates of a molecule by using a weighted covariance matrix:
where 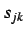 is the weighted covariance between the j'th and
k'th atomic coordinates,
is the weighted covariance between the j'th and
k'th atomic coordinates, 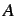 is the number of atoms,
is the number of atoms, 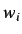 is the
weight of the i'th atom and
is the
weight of the i'th atom and 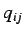 &
& 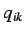 represent the j'th
and k'th coordinate (
represent the j'th
and k'th coordinate (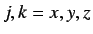 ) of the i'th atom and
) of the i'th atom and
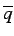 is the corresponding average value.
is the corresponding average value.
The weighted covariance matrix is obtained from different weighting
schemes for the atoms. Size schemes are proposed
- The unweighted case where
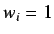
- atomic mass
- van der Waals volume
- Sanderson atomic electronegativity
- atomic polarizability
- electrotopological state indices
Depending on the weighting scheme different covariances matrices and
hence different principal axes are obtained. Essentially the WHIM
descriptors provide a variety of principal axes with respect to a defined atomic
property. For each weighting scheme, a set of statistical indices are
calculated on the atoms projected onto the principal axes (ie
principal components).
directional WHIM descriptors - these are univariate
statistical indices calculated on the scores of the individual
prinicpal components
- directional WHIM size - these are the eigenvalues
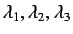 of the weighted covariance
matrix of the atomic coordinates and account for the
molecular size along the principal axes
of the weighted covariance
matrix of the atomic coordinates and account for the
molecular size along the principal axes
- directional WHIM shape - these are denoted as
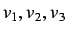 and are defined as
and are defined as
where 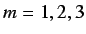
- directional WHIM symmetry - these are denoted by
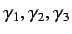 and are calculated as mean
information content on the symmetry along each component wrt
centre of the scores
and are calculated as mean
information content on the symmetry along each component wrt
centre of the scores
where 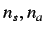 and
and 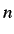 are the number of central symmetric
(along the m'th component), unsymmetric and total atoms of
the molecule.
are the number of central symmetric
(along the m'th component), unsymmetric and total atoms of
the molecule.
- directional WHIM density - these are denoted by
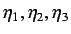 and are the inverse kurtosis
calculated from fourth order moments of the scores
(
and are the inverse kurtosis
calculated from fourth order moments of the scores
(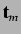 ) and describes the atom distribution and
density around
the origin and along the principal axes. Thus
) and describes the atom distribution and
density around
the origin and along the principal axes. Thus
The the 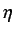 's relate to the quantity of unfilled space per
projected atom - higher values of
's relate to the quantity of unfilled space per
projected atom - higher values of 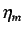 indicate larger
values of unfilled space
indicate larger
values of unfilled space
This for each weighting scheme we get a set of 11 directional
whim descriptors (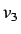 is excluded since it is a linear
combination of
is excluded since it is a linear
combination of 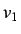 and
and 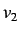 ) giving a total of 66
directional WHIM descriptors
These are calculated by combining the directional WHIM descriptors
) giving a total of 66
directional WHIM descriptors
These are calculated by combining the directional WHIM descriptors
- WHIM size - these consist of 3 descriptors representing
the total dimensions of the molecule
- WHIM shape - this is defined as
where 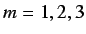 and
and
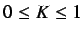 .
We only retain 3
.
We only retain 3 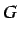 descriptors (
descriptors (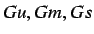 ) - that is those descriptors
for the unitary, mass and electrotopological weighting
schemes (since these are the only ones where the symmetry
values are different)
) - that is those descriptors
for the unitary, mass and electrotopological weighting
schemes (since these are the only ones where the symmetry
values are different)
- WHIM symmetry - this accounts for the total molecular
symmetry and is defined as
Thus 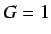 when the molecule shows a central symmetry
along each axis and tends to 0 when there is a loss of
symmetry along at least one axis
when the molecule shows a central symmetry
along each axis and tends to 0 when there is a loss of
symmetry along at least one axis
- WHIM density - describes the total density of atoms in
a molecule and is defined as
Thus for each weighting scheme there are 5 global WHIM
descriptors plus the 3 symmetry descriptors giving a total of 33
global WHIM descriptors.




Next: Bibliography
Up: Molecular Descriptors
Previous: 3D MoRSE[15,10]
Contents
2003-06-16
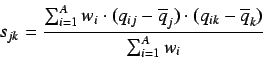
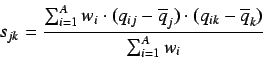
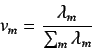
![\begin{eqnarray*}
\gamma^{'}_{m} & = & - \left[ \frac{n_s}{n} \cdot \log_2
\fr...
...} \right) \right] \\
\gamma_m & = &\frac{1}{1+\gamma^{'}_{m}}
\end{eqnarray*}](img108.png)